Roster Geometry and Resilience: Salary-Weighted Lineup Connectivity Predicts Playoff Stability

By Luke Blommesteyn, Yuvraj Sharma, and Lucian Lavric • Accepted to Carnegie Mellon Sports Analytics Conference

This page is a web adaptation of the paper - lighter commentary, same methods and results.

Abstract

We test whether the network geometry of NBA rosters, namely how salary resources are distributed across players who actually share the court, predicts playoff stability. Prior work links payroll level to outcomes or analyzes in-game pass networks. It rarely ties salary allocation to lineup connectivity or evaluates resilience to disruptions. We model each team-season as a salary-weighted, shared-possession network: nodes are players with size proportional to salary share, and edges capture co-presence intensity. We compute topology features (salary dispersion, salary assortativity, community structure, centralization, edge concentration) and define a Roster Resilience Score via robustness simulations that remove stars, role players, or community connectors, then score predicted drop from a model trained on intact networks.

Using public data from Basketball-Reference and Cleaning the Glass for 2020–21 through 2024–25 (149 team-seasons), we ask whether topology improves prediction of ordinal playoff advancement beyond a strength control. With salary-true features and leave-one-season-out cross validation, the full topology model raises Macro‑F1 from 29.0% to 31.3%. We release a reproducible pipeline covering data build, modeling, and figures.

Introduction

NBA front offices build rosters under a cap and many constraints. Payroll level correlates with success, yet two gaps remain. First, salary dispersion is usually studied without regard to who plays with whom. Second, network studies often focus on ball movement, not roster structure under cap realities. We propose a roster-level network view that weights players by salary share and connects only those who share possessions. This makes it possible to study geometry such as centralization, modularity, and assortativity, and to evaluate resilience to player losses.

Research Questions

RQ1: Do salary-network topology features predict playoff advancement beyond team strength?
RQ2: Which topology patterns relate to higher RRS?
RQ3: Do close or late, leverage-weighted edges improve explanatory power over unweighted co-presence?

Contributions

A roster network formulation that joins salary topology with who actually plays together.
A stress-test metric, the RRS, via systematic node removal.
A preregistered-style predictive evaluation with season-wise cross validation.
A fully reproducible pipeline.

Why this angle? Payroll matters, but where it shows up on the floor matters too. We measure that structure directly.

Related Work

Salary and performance studies examine aggregate spend. Basketball network analyses capture interaction patterns but not salary topology. Network robustness research shows that structured node removal can reveal vulnerability. We combine these ideas by linking salary topology to lineup connectivity and by stress testing roster graphs, using public sources throughout.

Data

We study NBA team-seasons from 2020–21 through 2024–25, for a total of 149 team-seasons.

Lineups and possessions

We use lineup and four-factor tables from Cleaning the Glass. Positions and possessions reconstruct on-court units. We compute co-presence counts for each pair of teammates and aggregate lineup Off and Def points per possession to a team-season strength proxy.

Salaries

We obtain player and team salary tables from Basketball-Reference and normalize to within-team salary shares.

Labels

We assemble playoff advancement labels from Basketball-Reference postseason brackets.

Data pipeline

Parse lineups into possession-weighted on-court units.
Merge salaries and normalize to team share per player.
Compute co-presence counts $c_{ij}$ and player possessions $n_i$.
Build graph $G=(V,E,w)$ with $w_{ij}=c_{ij}/\max(n_i,n_j)$ and threshold low-minutes nodes.
Compute topology features: salary dispersion, salary assortativity, community structure, centralization, and edge concentration.
Aggregate lineup Off and Def PPP to team NR and attach playoff labels.
Export leave-one-season-out splits and freeze seeds and hyperparameters.

Scope sanity check: five seasons, public-only sources, and deterministic builds so you can reproduce the aggregates.

Methods

Skimming? The trick is simple: weight players by salary share, connect only who actually play together, then test how fragile that shape is.

Network construction

Let $V$ be players with at least 300 possessions. For players $i$ and $j$, define the bounded co-presence intensity

$$ w_{ij} = \frac{\text{shared\ poss}_{ij}}{\max(\text{poss}_i,\text{poss}_j)} \in [0,1]. $$

Node size $s_i$ equals the player's salary share. A leverage-weighted variant $\tilde{w}_{ij}$ that up-weights close or late contexts is straightforward once leverage flags are integrated.

Topology features

Salary dispersion: Gini and top-$k$ share for $k\in\{1,2,3\}$.
Salary assortativity: weighted Pearson correlation of salary shares across edges $(i,j)$ using weights $w_{ij}$.
Community structure: modularity $Q$ and the coefficient of variation of community sizes.
Centralization: Freeman degree centralization with edge weights.
Edge concentration: fraction of total $w$ captured by the top five and top ten edges.

Performance proxy for stress tests

We fit a standardized ridge regression that maps intact topology features to team NR,

$$ \widehat{\mathrm{NR}} = f_\theta(x),\qquad f_\theta \in \{\text{Ridge}\}. $$

This proxy is used only to score stress-test perturbations consistently.

Robustness simulations and RRS

We remove, in turn, the highest-degree node, a mid-salary node, and the highest-betweenness node. After each removal we recompute features and score with $f_\theta$. Let $\Delta_s$ be the drop relative to intact,

$$ \mathrm{RRS} = 1 - \mathbb{E}_s\!\left[\frac{\Delta_s}{\left|\widehat{\mathrm{NR}}^{\,\text{intact}}\right|+\varepsilon}\right],\quad \varepsilon=10^{-3}. $$

We use winsorization in sensitivity checks when $\widehat{\mathrm{NR}}^{\text{intact}}$ is near zero.

Predictive modeling of playoff advancement

We predict ordinal playoff rounds $y\in\{0,1,2,3,4\}$, where 0 indicates missed playoffs and 4 indicates champion. We fit a multinomial logit as a robust ordinal surrogate with season-wise standardization. We evaluate with leave-one-season-out cross validation and report Macro‑F1, Accuracy, and mean absolute error of expected round.

Ablations. (A) Strength control only (NR). (B) Control plus salary dispersion. (C) Control plus connectivity features, including salary assortativity. (D) Full topology.

Pre-registered analysis plan

Before training we fix the feature list and thresholds, cross validation splits, ablation order and metrics, and a small hyperparameter grid for ridge and multinomial logit.

Results

TL;DR: topology adds signal. Connectivity lifts Macro‑F1 ~2–3 pts over a strength-only control; mixing salaries across connected lineups (negative assortativity) aligns with robustness.

Hard takeaways: (1) Connectivity beats a strength-only control. (2) Negative salary assortativity (mixing salaries across connected lineups) correlates with resilience. (3) Lower edge concentration = fewer single points of failure.

Incremental predictive value

Model	Macro-F1	Accuracy	MAE
A: Controls only	29.0	57.6	0.656
B: + Salary dispersion	26.5	53.1	0.651
C: + Connectivity	31.9	54.7	0.665
D: + Full topology	31.3	54.3	0.663

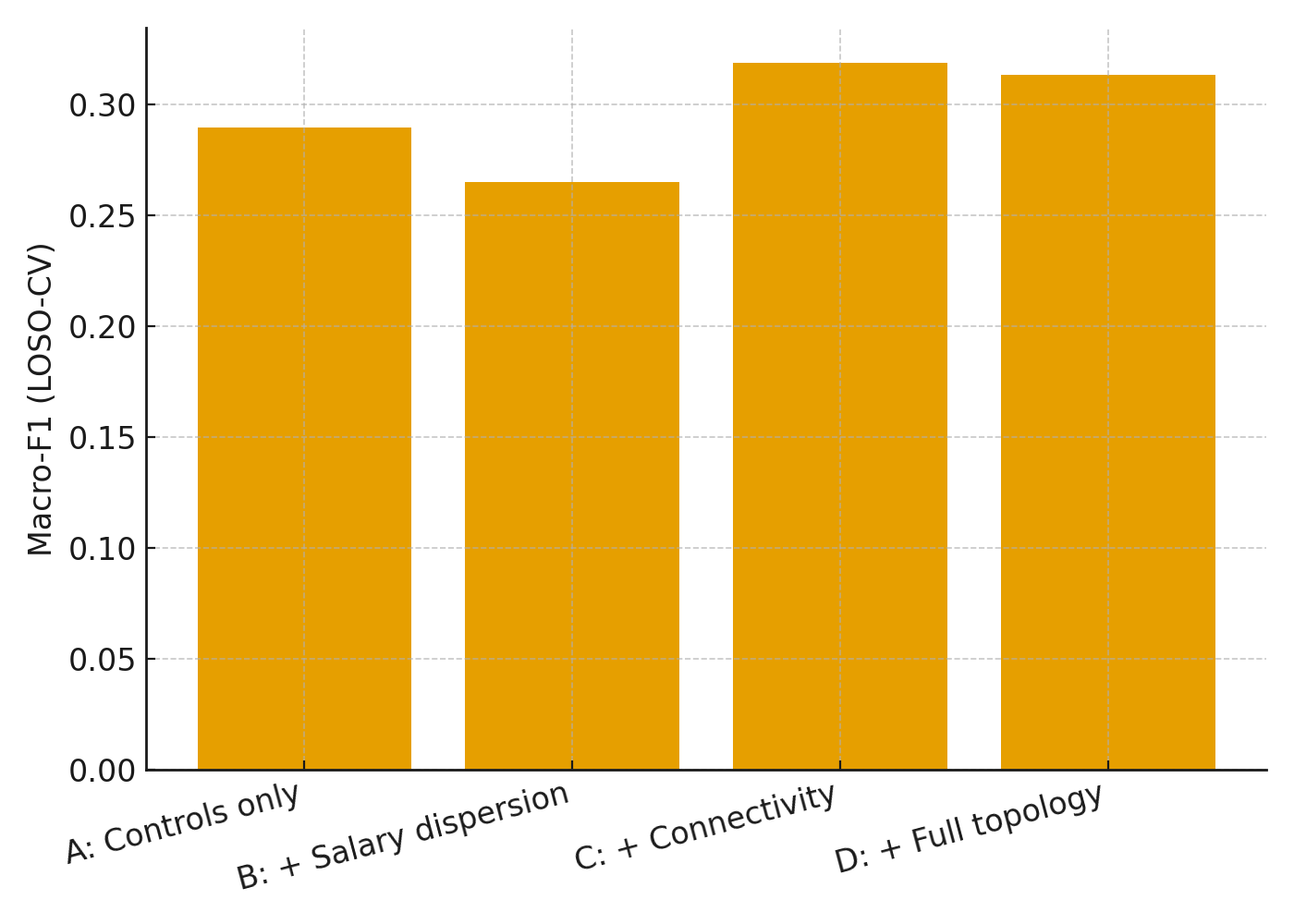
Ablation Macro‑F1 across models with leave‑one‑season‑out cross‑validation (salary‑true features) — Ablation Macro‑F1 by model (LOSO cross‑validation)

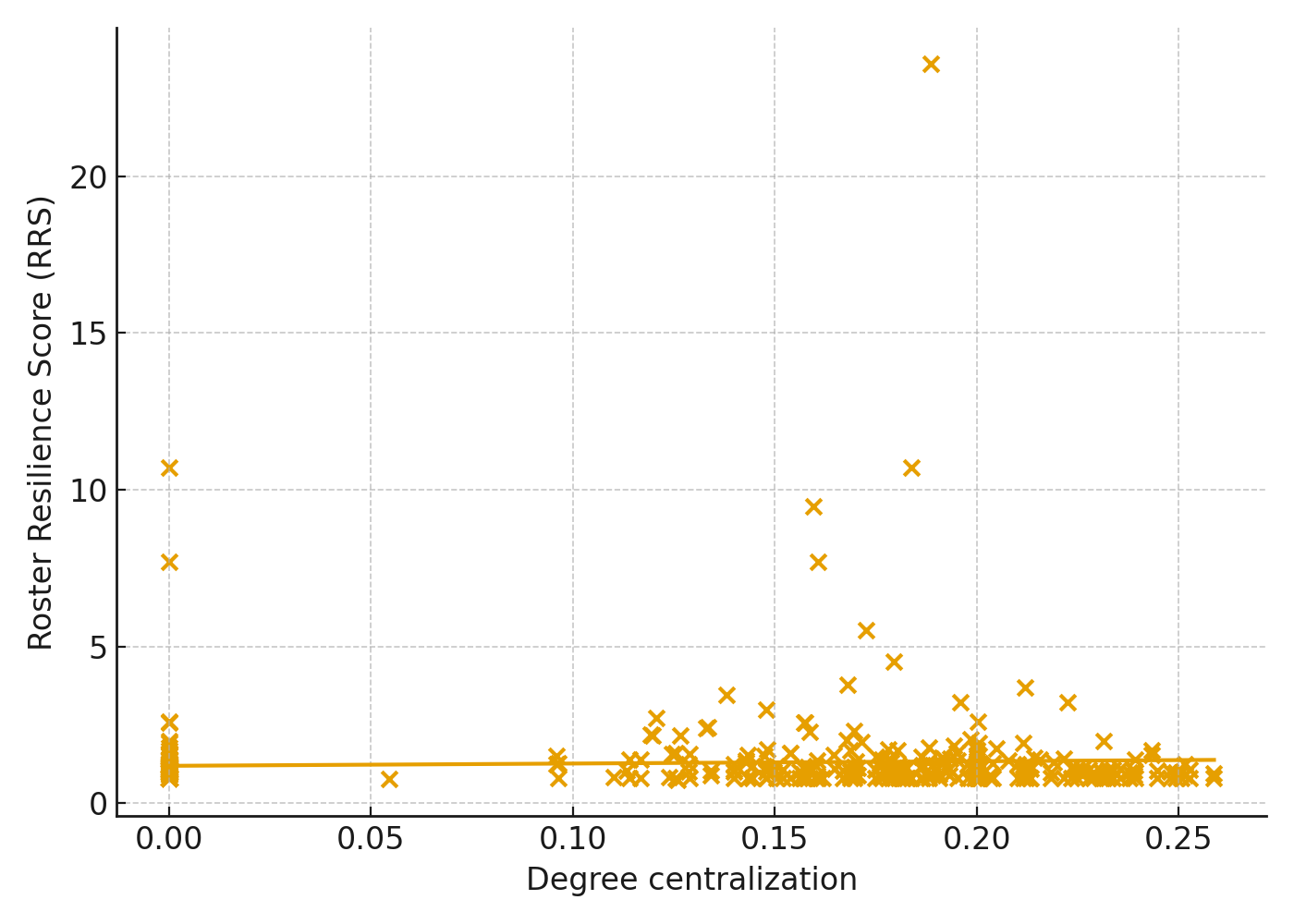
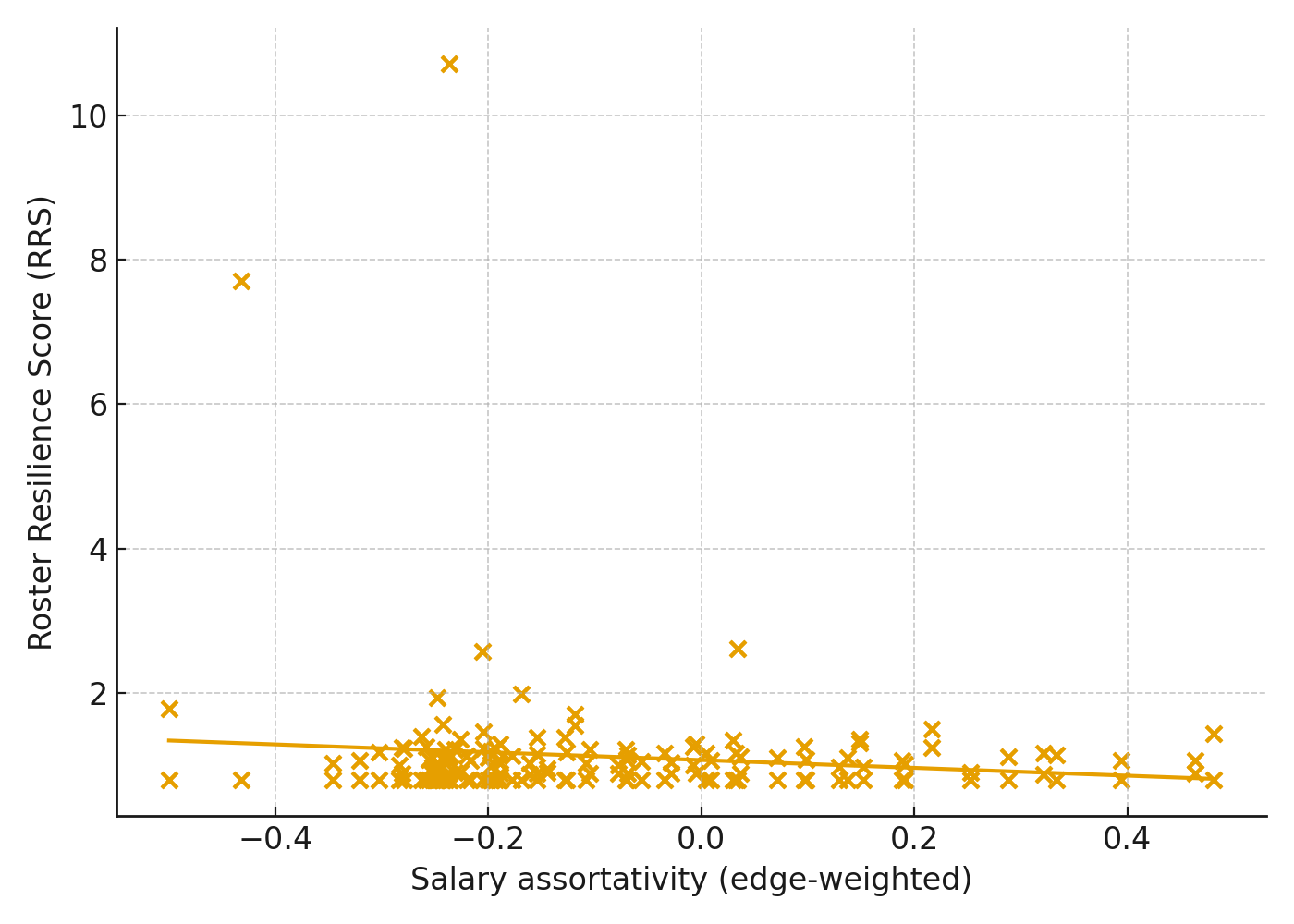
Resilience and topology based on RRS

When RRS is available, the association with degree centralization is weak, while salary assortativity is negatively related to RRS. This suggests that mixing salaries across connected lineups aligns with robustness to simulated disruptions.

Roster Resilience Score versus degree centralization — (a) RRS versus degree centralization

Roster Resilience Score versus salary assortativity — (b) RRS versus salary assortativity

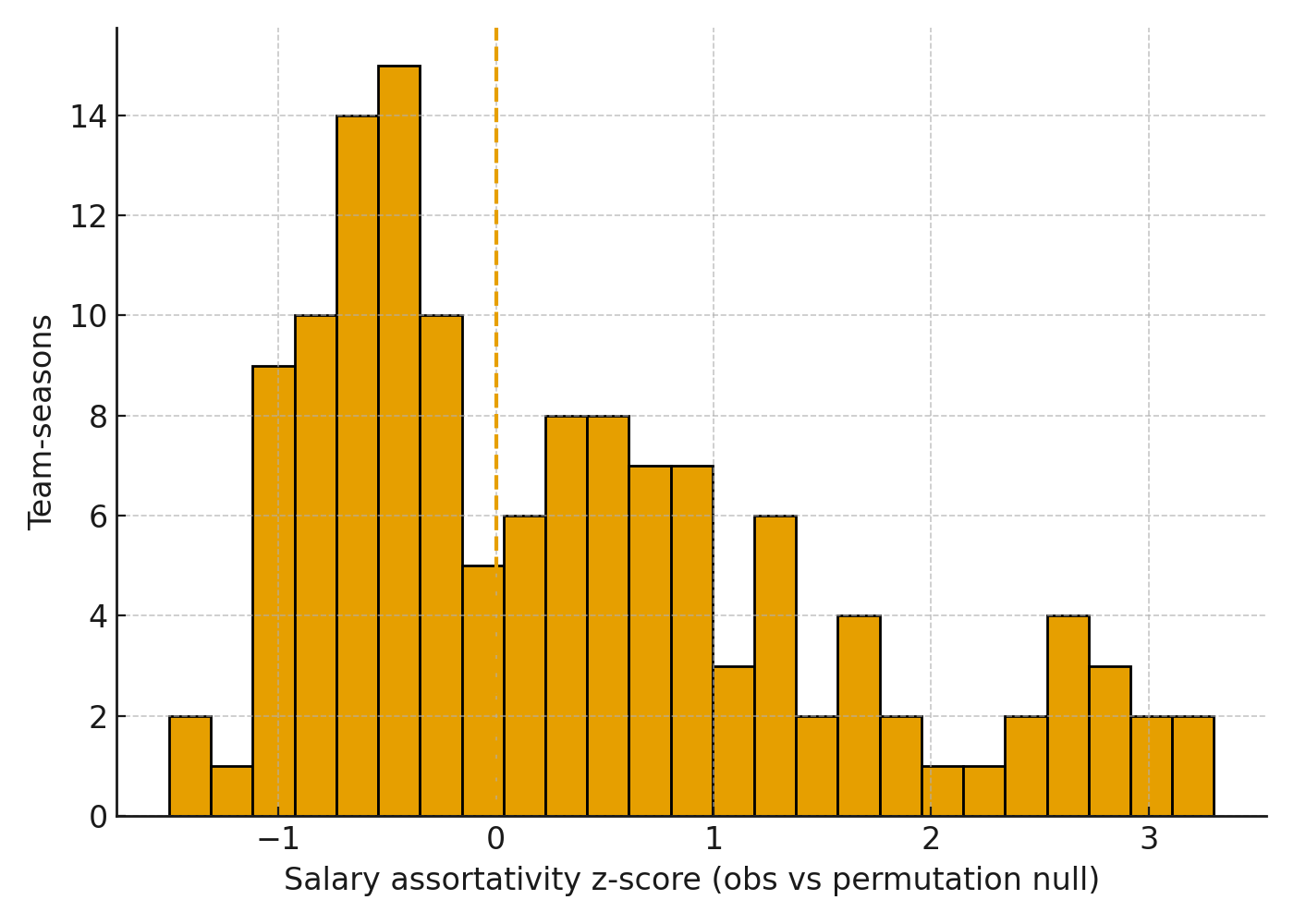
Falsification and outcome corroboration

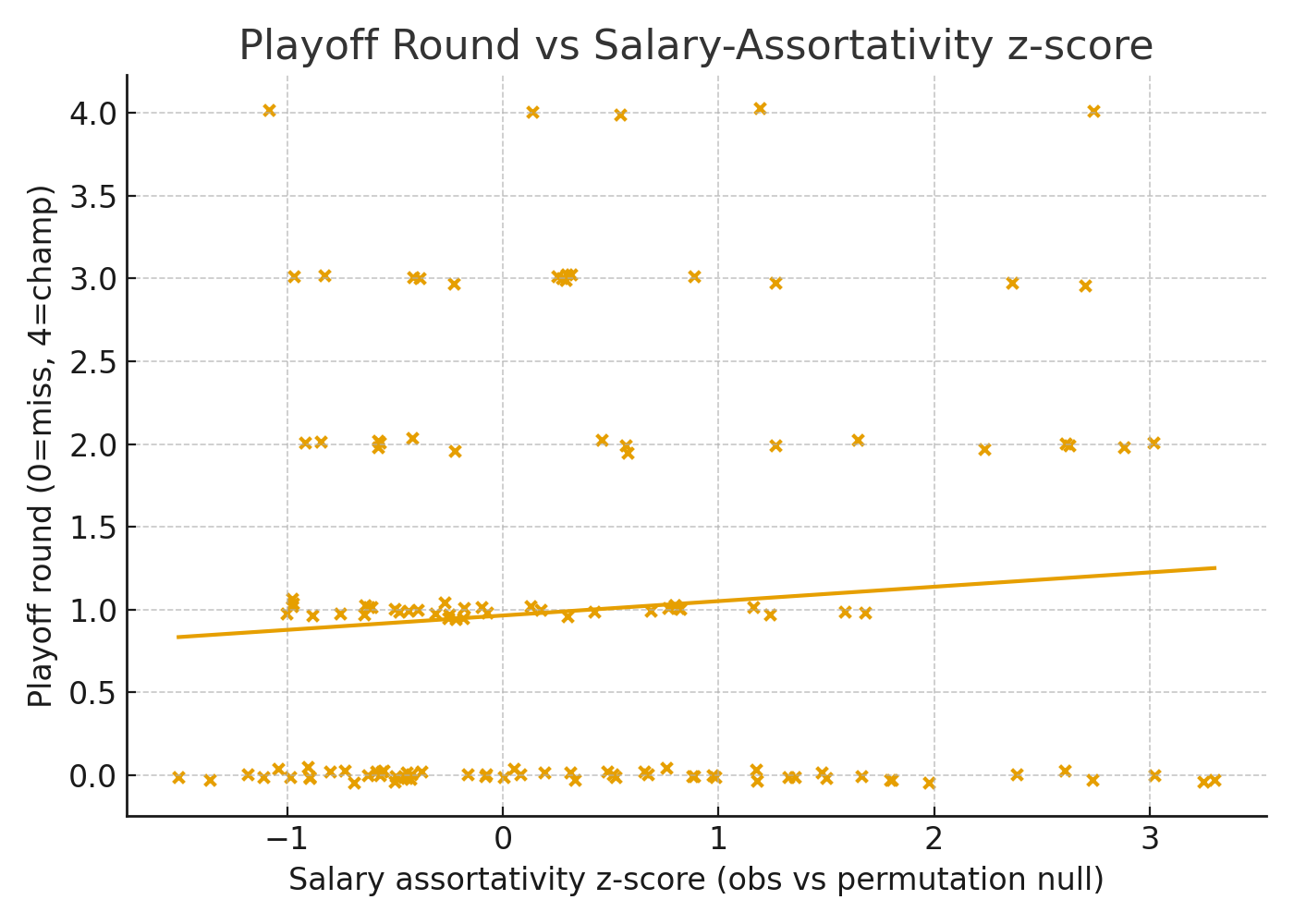
We test whether observed salary assortativity could arise by chance. For each team-season we hold the lineup graph fixed and randomly permute salary shares across nodes, then compute a z-score of observed assortativity relative to the permutation distribution. We also relate structure directly to outcomes: teams with more negative z-scores tend to reach later rounds.

Distribution of salary assortativity z-scores relative to a within-team permutation null — Permutation null: salary assortativity z-scores

Playoff round versus salary assortativity z-score with jitter and OLS fit — Playoff round versus salary assortativity z-score

Assortativity deciles for a managerial view

Sorting team-seasons into deciles by observed salary assortativity shows that lower-assortativity deciles, which imply more cross-salary mixing, advance further on average.

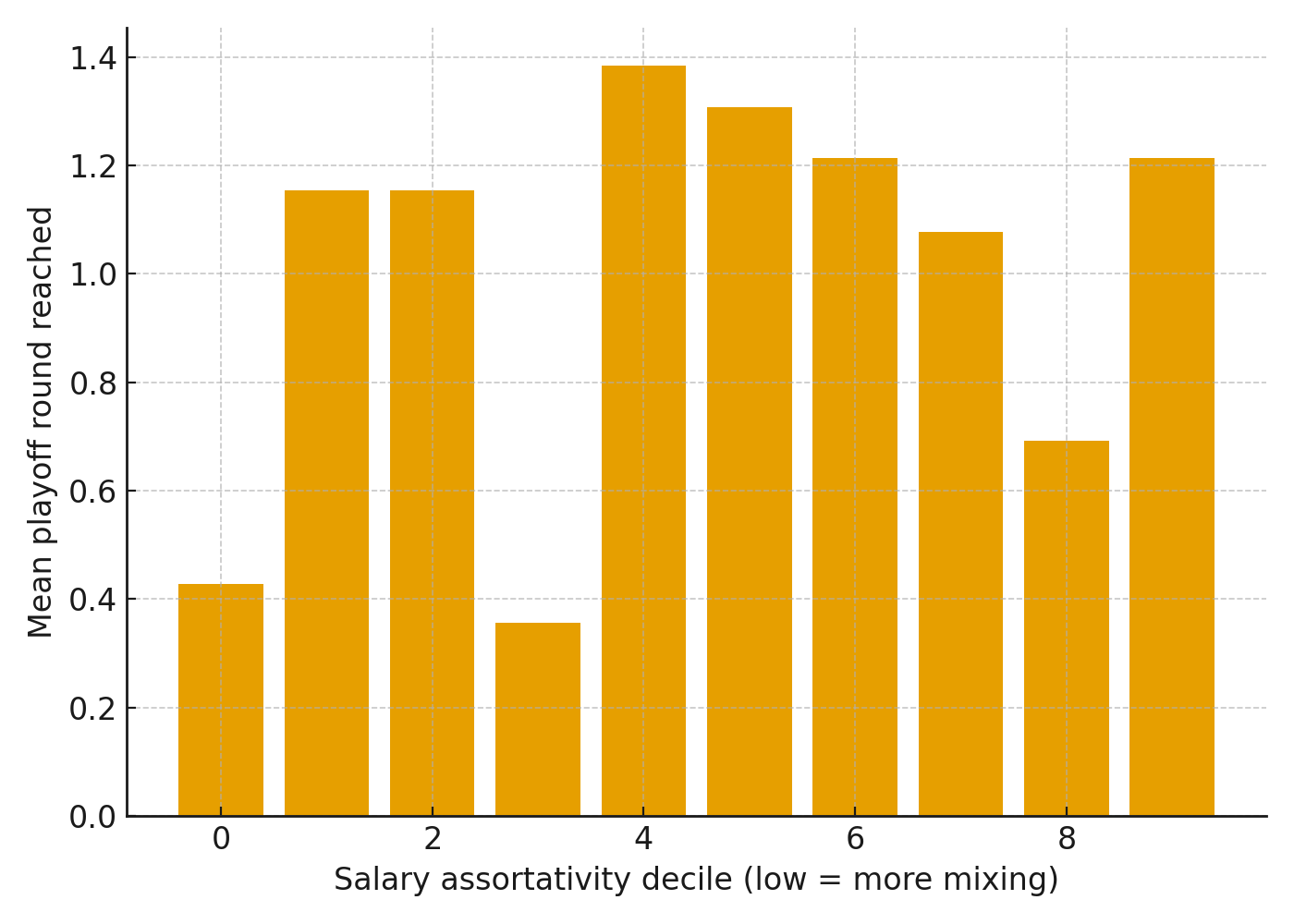
Mean playoff round by salary assortativity decile

Case studies of network geometry

Two anonymized team-seasons with similar expected playoff round from the ordinal model but different topology: one star-centered with high edge concentration and one more distributed with balanced communities. The latter aligns with a higher resilience profile.

Exemplar roster network A: star-centered topology with concentrated edges — Exemplar roster network (A)

Exemplar roster network B: distributed topology with balanced communities — Exemplar roster network (B)

Model diagnostics

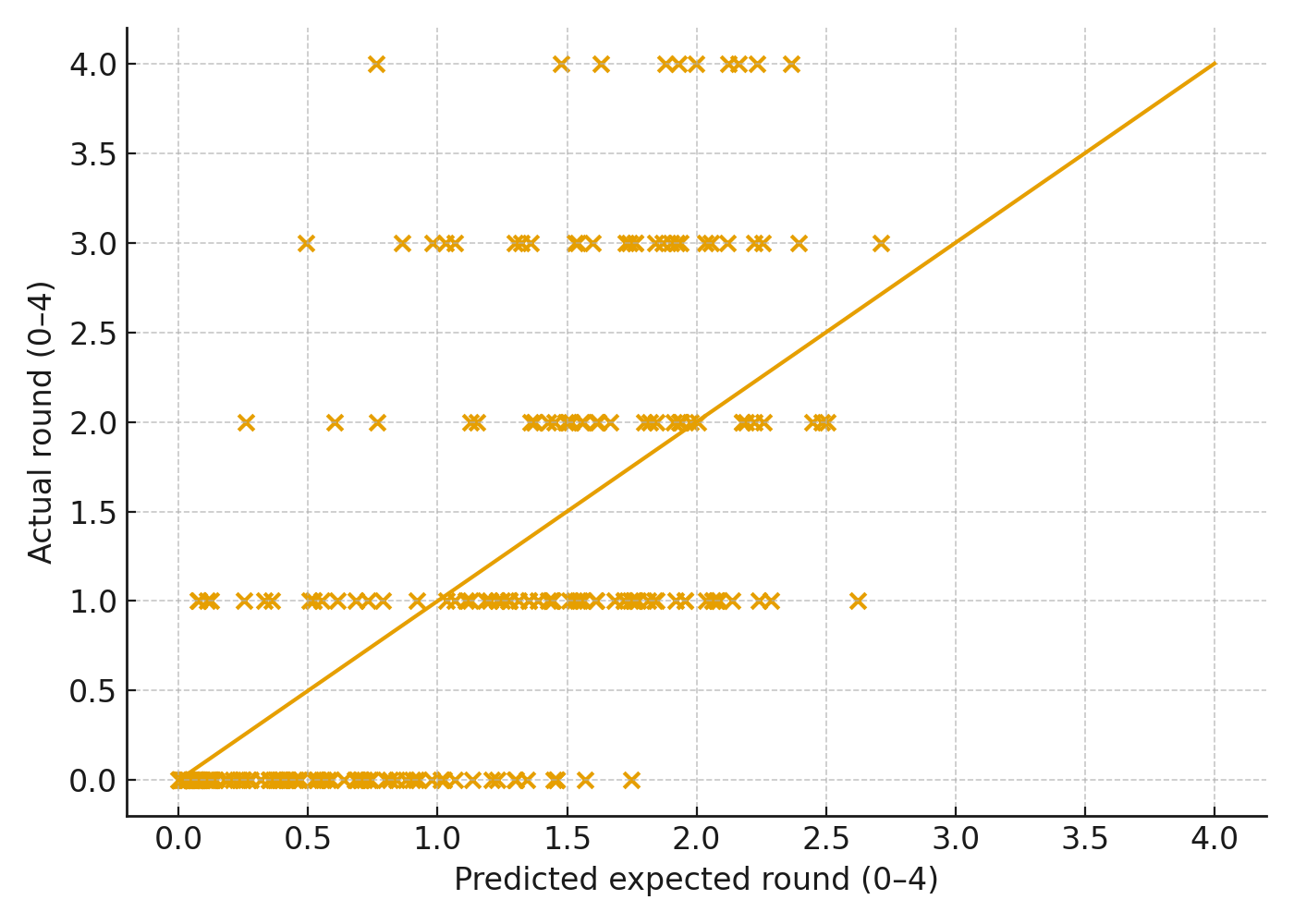
Calibration of expected playoff round versus actual with leave-one-season-out aggregation — Calibration of expected round vs actual

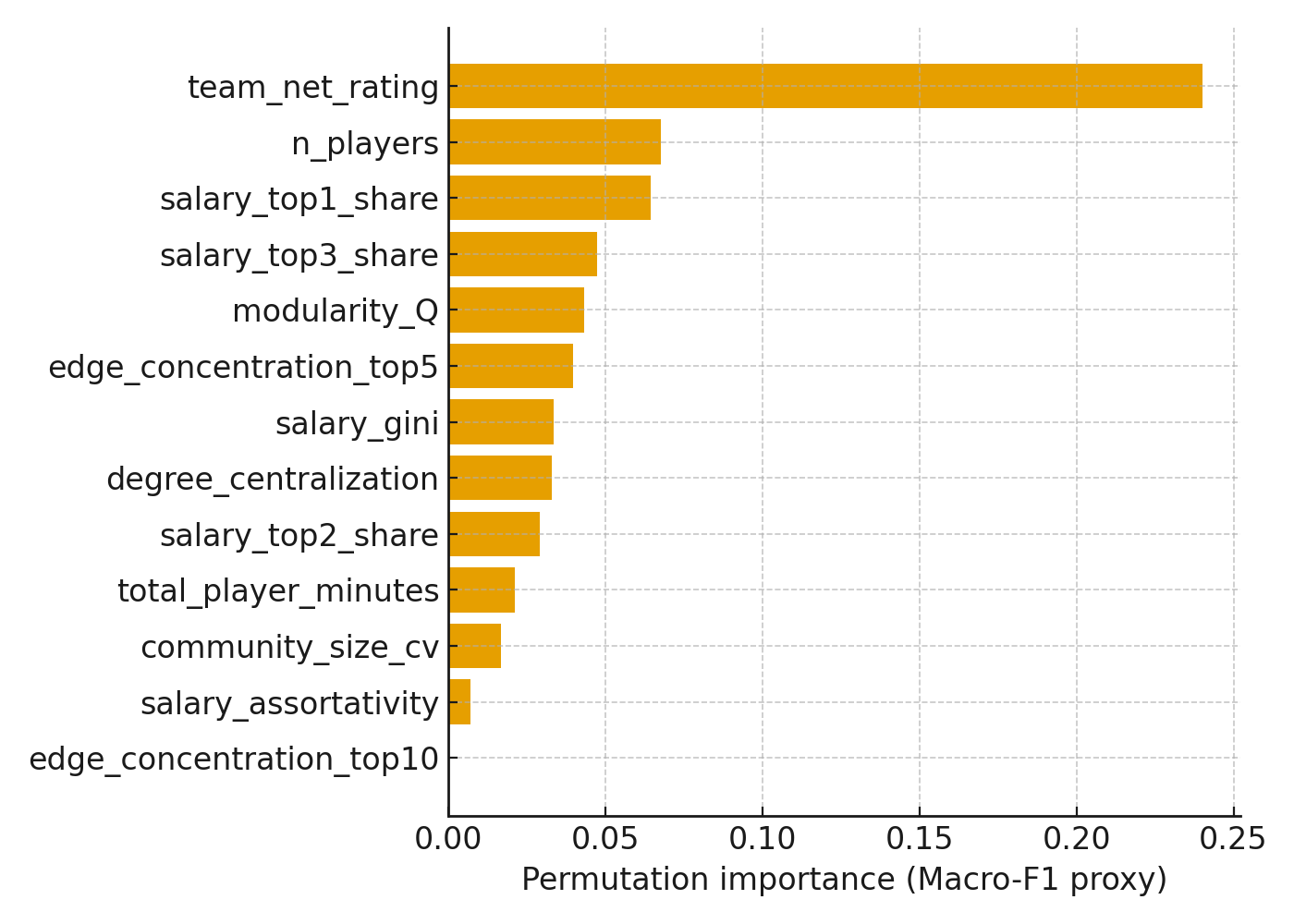
Permutation importance for the full playoff model with salary-aware topology — Permutation importance for the full model

Threats to validity

Salary data: Name resolution can miss two-way or ten-day players. We report matched counts and run strict and lenient variants.
Leverage: Edges are not yet leverage weighted. A close or late variant is a planned ablation.
Confounding: Minutes, role, and pay correlate. We include NR as a strength control and report ablations.
Measurement: Co-presence intensities abstract from play types. Community structure is coarse.
Generalization: The study covers five seasons and 149 team-seasons. We prefer regularization and season-wise cross validation.
RRS scaling: When $|\widehat{\mathrm{NR}}^{\text{intact}}|$ is near zero, normalization can inflate RRS. We winsorize in sensitivity checks.

Ethics and transparency

All data were obtained from public sources: Basketball-Reference and Cleaning the Glass. We comply with the providers' terms of use. We release code, seeds, and environment files so readers can reproduce results with publicly accessible exports.

Reproducibility statement

We provide data-processing scripts for lineup graphs and salary merges, pinned environment files, a Makefile to regenerate all tables and figures, and documented loaders for Basketball-Reference and Cleaning the Glass exports.

Conclusion

We link salary-weighted roster topology to lineup connectivity and show that connectivity adds information beyond team strength. Across five seasons, topology features, especially salary assortativity and edge concentration, improve ordinal playoff prediction over a strength-only control. A permutation falsification confirms that observed negative assortativity is not a byproduct of roster size or lineup coverage. Outcome analyses based on playoff rounds support the same pattern. For practice, front offices can stagger high salaries across lineups and reduce edge concentration. These steps can improve robustness without raising total payroll. Future work should incorporate leverage-weighted edges, expand seasons and leagues, and add richer controls such as injuries and rest.

References

D. J. Berri and M. B. Schmidt, Stumbling on Wins. FT Press, 2010.
R. Fort and J. Quirk, “Cross-subsidization, incentives, and outcomes in professional team sports leagues,” Journal of Economic Literature, vol. 33, no. 3, pp. 1265–1299, 1995.
J. H. Fewell, D. Armbruster, J. Ingraham, A. Petersen, and J. S. Waters, “Basketball teams as strategic networks,” PLOS ONE, vol. 7, no. 11, p. e47445, 2012.
R. Albert, H. Jeong, and A.-L. Barabási, “Error and attack tolerance of complex networks,” Nature, vol. 406, no. 6794, pp. 378–382, 2000.
Basketball-Reference.com, “NBA statistics and history,” basketball-reference.com, accessed 2025.
Cleaning the Glass, “NBA lineup and four-factor statistics,” cleaningtheglass.com, accessed 2025.