Elixir Under Uncertainty: Mechanics-Grounded Risk-Sensitive Control for Clash Royale

The seven-elixir freeze

Double elixir, forty seconds on the clock. You’re up a tower. You’re sitting on seven elixir and your opponent just slammed a five-cost into the other lane. Do you push now while they’re tapped out, or hold and protect the lead? Every Clash Royale player knows that half-second of paralysis, and most of us resolve it on vibes.

Here’s the thing though. You know more than it feels like you know. They spent five, so right now they have at most five. The clock phase fixes how fast that refills. You’re ahead, so a blown push costs you more than a good one wins. None of that needs you to read their hand or mine a million ladder replays. It falls straight out of the game’s own rules.

So this note takes that freeze and turns it into something you can compute. It treats elixir trading as risk-sensitive decision-making under partial observability, using only the official mechanics and card catalogue as data. And it turns out the gut heuristics, bank when ahead, take variance when behind, probe when it’s cheap, are the mathematically right shape. What you get at the end is a go/no-go threshold you can carry onto ladder, not a black box.

Abstract

This is a mechanics-grounded framework for elixir trading in Clash Royale. Using only the game's rules (elixir regeneration, deck cycle, timing) and the card catalogue (costs, base stats) as data, I cast decision-making as risk-sensitive partial observability over the opponent's elixir, hand rotation, and archetype. I derive structural results, namely potential-based shaping invariance, elixir belief bounds after plays, scoreline/clock-aware risk thresholds, lane decoupling via shadow prices, value-of-information guarantees, belief-compression error bounds, and delay robustness, and specify algorithms that exploit them. I also define mechanics-consistent testbeds that benchmark policies without relying on large-scale ladder logs. The result is a data-light, actionable approach to risk-aware control in real-time card battlers.

The short version

Quick start

• Ahead late? Raise the risk threshold \(\kappa^\star\), bank elixir, and make them commit first.
• Behind? Lower \(\kappa^\star\), lean into variance, and use probes to surface whatever counter is blocking your win condition.
• Two lanes? Spend where marginal tower damage per elixir beats the shadow price \(\mu\). Split when both lanes price out about the same.
• Always track reveals. Update the elixir envelopes and hand belief after every play. The tighter your belief, the harder you can commit.

The game-theory lens

Math & ML TL;DR

Introduction

Competitive Clash Royale comes down to trading elixir for tempo, value and tower damage, while only partly seeing what your opponent has. Strong players already do this. They hold beliefs about opponent elixir, hand cycle and archetype, and they adjust aggression by clock phase and scoreline, protecting a lead or chasing one.

I wanted to write that reasoning down. So I formalized the game as a risk-sensitive POMDP, proved decision-structure properties like thresholds, decouplings and information value, specified algorithms that run on compact belief features, and evaluated on testbeds that need no match logs.

Contributions

• Mechanics-grounded formulation: POMDP with elixir regen, cycle, and partial observability over opponent elixir/hand/archetype.
• Structural results: shaping invariance; elixir belief bounds after plays; risk-threshold monotonicity; lane decoupling via a shadow price; greedy VOI guarantees; belief-compression regret; delay robustness.
• Algorithms: belief-augmented policy with a risk dial; shadow-price control; greedy probing for information.
• Testbeds: mechanics-consistent, data-light benchmarks (closed-form or tiny DPs) for reproducible evaluation without large logs.

The data

Only the official mechanics and catalogue parameters. The elixir regeneration schedule for normal, double and triple, the 10-elixir cap, the 8-card deck with its 4-card FIFO hand, and card costs and base stats like HP, DPS, range and speed. No match logs anywhere. Validating against real telemetry is future work.

Glossary (fast definitions)

Mechanics & Assumptions

I study decision times \(t = 0,1,\dots\) with actions of "play a legal card at a placement" or "wait." Between decisions, physics evolves deterministically at the macro level and elixir regenerates.

Assumptions

• Elixir process. Each player has elixir \(e_t \in [0,10]\). The regeneration rate \(g_t\) is piecewise constant by clock phase (normal/double/triple).
• Cycle. Hand is a size-4 FIFO sample from an 8-card deck; after playing a card, it moves to the back and a new card is drawn immediately.
• Observations. I observe public board state and opponent plays with costs; opponent elixir \(e^O_t\), hand \(\mathcal{H}^O_t\), and archetype \(a\) are hidden.
• Rewards. Per-step reward aggregates crown/tower HP change and tempo; a potential term may reattribute credit to elixir trades.
• Legalities. Placement legality and hand constraints are respected; actions with cost \(> e_t\) are infeasible.

Plain English. The only assumptions are the real game rules: how fast elixir comes back, the 10-cap, and how deck cycling works. That’s enough to reason about the opponent without ever seeing their hand.

Formal Model

Let \(\mathcal{M} = (\mathcal{S}, \mathcal{A}, \mathcal{O}, T, \Omega, R, \gamma)\) be a POMDP with state \(s_t = (x_t, z_t)\), public component \(x_t\) (board, clock, your elixir/hand), hidden component \(z_t = (e^O_t, \mathcal{H}^O_t, a)\), observation \(o_t = f(x_t)\). The action \(u_t \in \mathcal{A}\) is either \emph{hold} or \emph{play} \((c, \ell)\) for a legal card \(c\) and placement \(\ell\). The transition couples (i) elixir updates \(e_{t+1} = \min\{10, e_t - \mathrm{cost}(u_t) + g_t\}\); (ii) cycle updates; (iii) board evolution.

Risk-sensitive criteria

I consider:

\[ J_{\lambda}(\pi) = \mathbb{E}[R] - \lambda \, \mathrm{Var}(R), \] \[ \max \; \mathrm{CVaR}_{\alpha}(R) = \max\, \mathbb{E}[R] - \lambda\, \rho_{\alpha}(R),\qquad \sup_{\pi} \inf_{\delta \in \mathcal{D}} \mathbb{E}_{\delta}[R]. \]

I use a scoreline/clock-aware risk parameter \(\lambda_t = \lambda(\text{lead}, \text{clock})\).

Structural Results

Each result below is a formal statement followed by what it means mid-match. The math carries the guarantee. The note carries the move.

Potential-based shaping invariance on beliefs

Theorem. Let the belief-MDP state be \((x_t, b_t)\) with belief \(b_t\) over \(z_t\). For any potential \(\Phi\), define \(r'_t = r_t + \gamma \Phi(x_{t+1}, b_{t+1}) - \Phi(x_t, b_t)\). A policy is optimal under \(r\) iff it is optimal under \(r'\).

Elixir belief support after an observed play

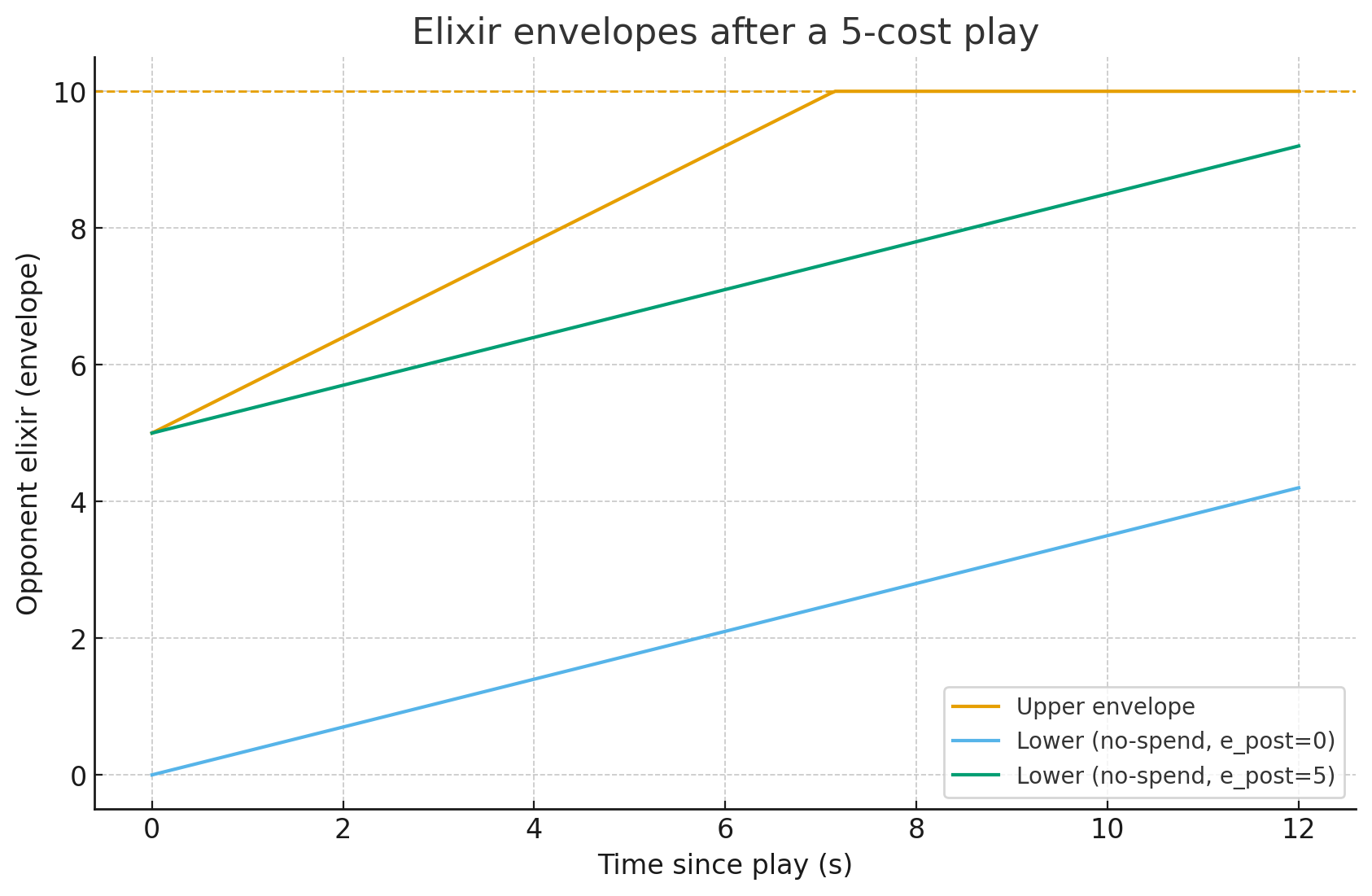
Theorem. Opponent plays a card of cost \(c\). Legality implies \(e^O_{t^-} \ge c\) and the post-play elixir satisfies \(e^O_{t^+} = e^O_{t^-} - c \in [0, 10-c]\). Regen on \((t, t+\tau]\) with rate in \([g_{\min}, g_{\max}]\) yields envelopes for \(e^O_{t+\tau}\).

Corollary: Tick-wise envelopes

With decision tick \(\Delta t\), \(k\) steps after the play: \(0 \le e^O_{t+k} \le \min\{10, (10-c) + k g_{\max} \Delta t\}\). Tighten the lower bound if they do not spend again.

Risk-threshold monotonicity

Theorem. Order actions \(\texttt{hold} \preceq \texttt{play}\) and let \(\kappa\) be a scalar risk index. If \(Q\) has increasing differences in \((\kappa, a)\), there exists a threshold \(\kappa^{\star}(b)\): play when \(\kappa \le \kappa^{\star}(b)\), hold otherwise.

Risk-aware push threshold

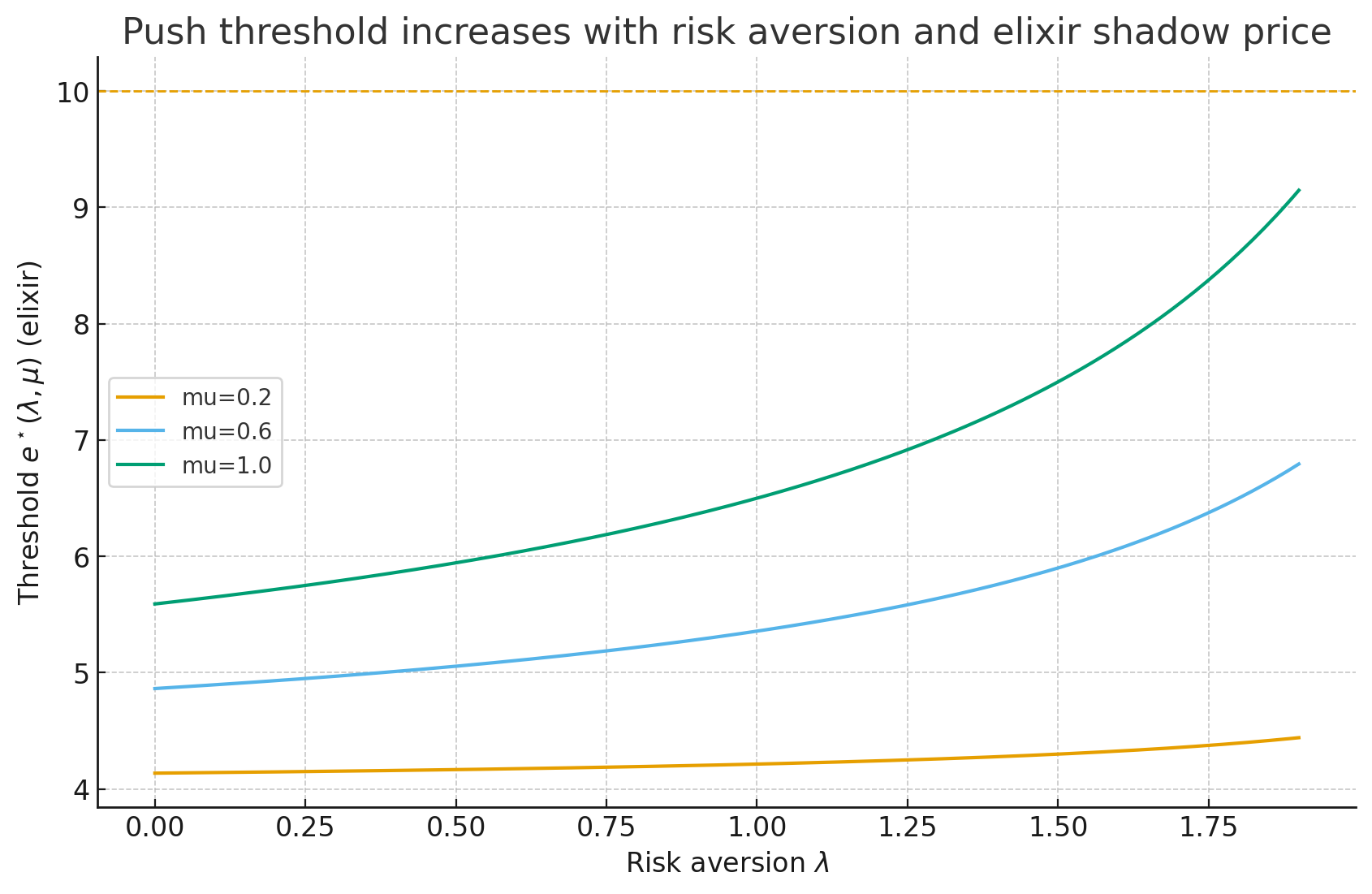
Proposition. For a push costing \(c\) with \(\mathbb{E}[R] = \alpha(e-c)+\beta\) and \(\mathrm{Var}(R) = \sigma^2(e-c)\), and elixir shadow price \(\mu\), if \(\alpha > \lambda \sigma^2\) then push iff \(e \ge e^{\star}(\lambda, \mu) = c + \frac{\mu c - \beta}{\alpha - \lambda \sigma^2}\).

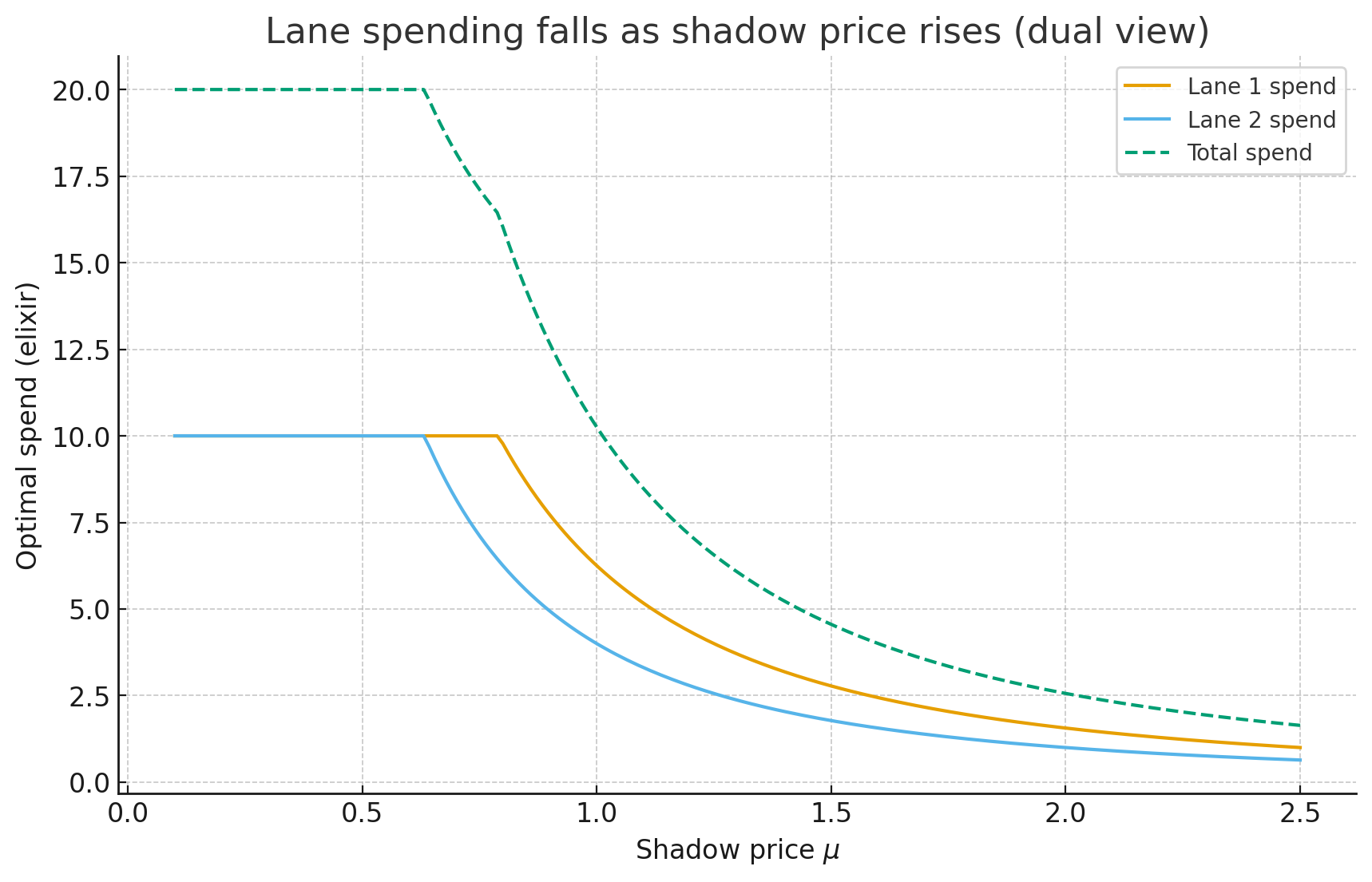
Shadow-price decoupling across lanes

Theorem. Relax the shared elixir budget with price \(\mu\); solve each lane separately with a per-elixir penalty. Bisection on \(\mu\) balances lanes and gives a dual upper bound.

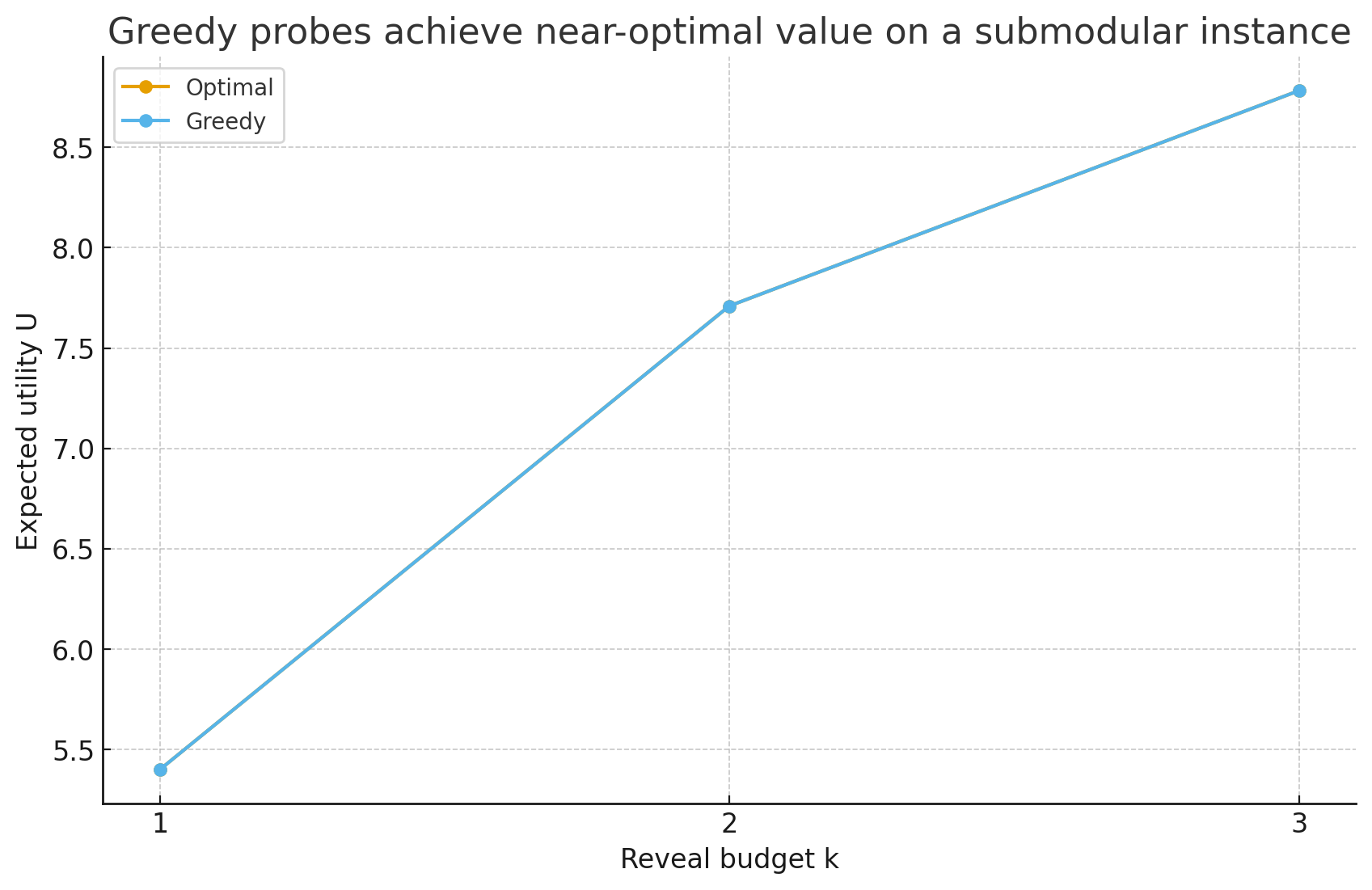
Greedy VOI under adaptive submodularity

Theorem. If expected return \(U\) is monotone and adaptively submodular in reveals, the greedy "max \(\Delta U\) per time" probe is a \((1-1/e)\)-approximation to the optimal \(k\)-reveal policy.

Belief compression regret

Theorem. If \(Q\) is Lipschitz in belief and the compressed belief has uniform error \(\epsilon\), then \(|J(\pi_{\phi}) - J(\pi_{\star})| \le \frac{2 \gamma L}{(1-\gamma)^2} \, \epsilon\).

Delay robustness

Theorem. With Lipschitz dynamics/rewards and latency \(\Delta \in [0, \delta]\), \(J(\pi_{\text{delay}}) \ge J(\pi) - O(L\delta)\).

Algorithms (provable or bounded)

Belief-Augmented Policy (BAP). Policy over compressed beliefs \(\phi(b_t)\) with a risk dial \(\lambda_t\). Use QMDP or one-step look-ahead; the belief compression theorem bounds suboptimality.

Shadow-price control. Tune \(\mu\) online (dual ascent) to balance lanes.

Risk schedule. Precompute \(\kappa^{\star}(\text{lead}, \text{clock})\) from tiny MDPs.

Greedy probing. Choose micro-plays with maximal \(\Delta \mathrm{CVaR}/\Delta t\) or \(\Delta U/\Delta t\) with safety guarantees.

Belief-Augmented Policy with Risk Dial (sketch)

Initialize policy π_θ, belief filter B, risk schedule λ_t
for each decision time t:
  b_t ← B(history)
  φ_t ← φ(b_t)
  κ_t ← κ(lead, clock)  # risk index
  choose u_t ∈ argmax_u Q^risk(o_t, φ_t, u; κ_t)
  execute u_t, observe outcome, update B

Mechanics-Consistent Testbeds (data-light)

1. Elixir bank vs. push: two actions {hold, push} with stochastic opponent counter; yields explicit thresholds.
2. Two-lane knapsack: independent per-lane values with shared elixir; compare primal (shadow price) to the dual bound.
3. Reveal game: micro-plays reveal a card or tighten a lower bound on \(e^O\); compare greedy probing to the optimal \(k\)-reveal policy.

Notation

FAQ (Coach / Player)

I don't know their exact elixir. Can I still use this?

Yes. Use the envelopes from the elixir-bounds theorem and tighten them after each reveal.

When is a cheap probe worth it?

If it narrows their hand/elixir and unlocks your win-con timing, greedy probes are near-optimal.

How do I split lanes?

Spend where the value per elixir is highest given \(\mu\); adjust until total spend fits the budget.

I'm ahead with 45 seconds left.

Turn the risk dial up: wait for better trades and require a higher threshold \(e^{\star}\) before pushing.

What could be wrong with this

The assumptions here target macro elixir and cycle economics. I’m not claiming pixel-level fidelity. The structural results are robust to simulator details, but the numerical curves depend on stylized parameters. Extending to POSGs, meaning explicit opponent models, is straightforward, since the belief-MDP approach carries over. And none of this leans on large-scale ladder logs, so validating against real telemetry is still to do.

Ethics. This is analysis and a training aid. It isn’t meant for automating live ladder play.

Conclusion

Working from the mechanics alone gets you real structure: thresholds for policy, shadow prices for relaxing the coupling between lanes, and information-theoretic guidance under risk. All of it from data-light inputs, meaning just the rules and the catalogue. That makes the work reproducible, and it makes it usable as a coaching tool for real-time card battlers.

But the thing I actually took from this is smaller and more personal. That seven-elixir freeze at the top, the half-second of paralysis every player knows, was never a lack of information. Everything you needed was already on the screen. They spent five. The clock fixes the refill. You’re ahead. The math didn’t give me new knowledge so much as permission to trust what the rules were already telling me.

I suspect most gut feelings in games are like this. Not mysteries, just theorems nobody wrote down yet. The fun part is finding the next one.

Reproducibility Checklist

• Seeds and exact parameters for toy instances.
• Closed-form thresholds and small DP scripts for testbeds.
• Specification of the \(\lambda_t\) schedule and belief compression features.

Appendix (sketches)

Belief-MDP & shaping

Beliefs \(b_t\) over hidden state yield an MDP with state \((x_t, b_t)\). Shaped returns differ by a potential term; value functions shift by a constant, preserving optimal policies.

Risk-threshold monotonicity

With increasing differences in \((\kappa, a)\) and diminishing returns in elixir, the argmax set is non-decreasing in \(\kappa\); a threshold exists. Mean–variance and CVaR surrogates satisfy this.

Value of information

If expected return is adaptively submodular in reveals, greedy selection achieves \((1-1/e)\) of optimal for a reveal budget.

Belief compression

Lipschitz continuity plus the performance-difference lemma yields \(|J(\pi_{\phi})-J(\pi_{\star})| \le \tfrac{2\gamma L}{(1-\gamma)^2} \, \epsilon\).

Delay robustness

Model latency as adversarial timing within \([0,\delta]\). Value loss is \(O(L\delta)\) per step; geometric discounting gives the bound.